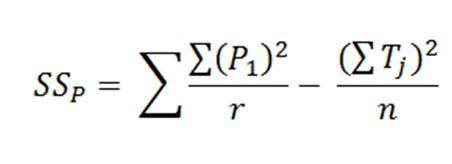BAB 9 ANALISIS REGRESI & ANALISIS KORELASI

A.    KORELASI 

1. PENGERTIAN KORELASI
 

Korelasi merupakan teknik analisis yang termasuk dalam salah satu teknik pengukuran asosiasi / hubungan (measures of association). Pengukuran asosiasi merupakan istilah umum yang mengacu pada sekelompok teknik dalam statistik bivariat yang digunakan untuk mengukur kekuatan hubungan antara dua variabel. Diantara sekian banyak teknik-teknik pengukuran asosiasi, terdapat dua teknik korelasi yang sangat populer sampai sekarang, yaitu Korelasi Pearson Product Moment dan Korelasi Rank Spearman. Selain kedua teknik tersebut, terdapat pula teknik-teknik korelasi lain, seperti Kendal, Chi-Square, Phi Coefficient, Goodman-Kruskal, Somer, dan Wilson.

Pengukuran asosiasi mengenakan nilai numerik untuk mengetahui tingkatan asosiasi atau kekuatan hubungan antara variabel. Dua variabel dikatakan berasosiasi jika perilaku variabel yang satu mempengaruhi variabel yang lain. Jika tidak terjadi pengaruh, maka kedua variabel tersebut disebut independen.

Korelasi bermanfaat untuk mengukur kekuatan hubungan antara dua variabel (kadang lebih dari dua variabel) dengan skala-skala tertentu, misalnya Pearson data harus berskala interval atau rasio; Spearman dan Kendal menggunakan skala ordinal; Chi Square menggunakan data nominal. Kuat lemah hubungan diukur diantara jarak (range) 0 sampai dengan 1. Korelasi mempunyai kemungkinan pengujian hipotesis dua arah (two tailed). Korelasi searah jika nilai koefesien korelasi diketemukan positif; sebaliknya jika nilai koefesien korelasi negatif, korelasi disebut tidak searah. Yang dimaksud dengan koefesien korelasi ialah suatu pengukuran statistik kovariasi atau asosiasi antara dua variabel. Jika koefesien korelasi diketemukan tidak sama dengan nol (0), maka terdapat ketergantungan antara dua variabel tersebut. Jika koefesien korelasi diketemukan +1. maka hubungan tersebut disebut sebagai korelasi sempurna atau hubungan linear sempurna dengan kemiringan (slope) positif.

Jika koefesien korelasi diketemukan -1. maka hubungan tersebut disebut sebagai korelasi sempurna atau hubungan linear sempurna dengan kemiringan (slope) negatif. Dalam korelasi sempurna tidak diperlukan lagi pengujian hipotesis, karena kedua variabel mempunyai hubungan linear yang sempurna. Artinya variabel X mempengaruhi variabel Y secara sempurna. Jika korelasi sama dengan nol (0), maka tidak terdapat hubungan antara kedua variabel tersebut. Dalam korelasi sebenarnya tidak dikenal istilah variabel bebas dan variabel tergantung. Biasanya dalam penghitungan digunakan simbol X untuk variabel pertama dan Y untuk variabel kedua. Dalam contoh hubungan antara variabel remunerasi dengan kepuasan kerja, maka variabel remunerasi merupakan variabel X dan kepuasan kerja merupakan variabel Y.

2. KEGUNAAN

            Pengukuran asosiasi berguna untuk mengukur kekuatan (strength) hubungan antar dua variabel atau lebih. Contoh: mengukur hubungan antara variabel:

-Motivasi kerja dengan produktivitas

-Kualitas layanan dengan kepuasan pelanggan

-Tingkat inflasi dengan IHSG

Pengukuran ini hubungan antara dua variabel untuk masing-masing kasus akan menghasilkan keputusan, diantaranya:

-Hubungan kedua variabel tidak ada

-Hubungan kedua variabel lemah

-Hubungan kedua variabel cukup kuat

-Hubungan kedua variabel kuat

-Hubungan kedua variabel sangat kuat

Penentuan tersebut didasarkan pada kriteria yang menyebutkan jika hubungan mendekati 1, maka hubungan semakin kuat; sebaliknya jika hubungan mendekati 0, maka hubungan semakin lemah.

3. ANALISIS KORELASI

3.1 Analisis Korelasi Parsial
 

Analisis korelasi parsial (Partial Correlation) digunakan untuk mengetahui hubungan antara dua variabel dimana variabel lainnya yang dianggap berpengaruh dikendalikan atau dibuat tetap (sebagai variabel kontrol). Nilai korelasi (r) berkisar antar 1 sampai -1, nilai semakin mendekati 1 atau -1 berarti hubungan antara dua variabel semakin kuat, dan sebaliknya. Nilai positif menunjukkan hubungan searah (X naik maka Y naik) dan nilai negatif menunjukkan hubungan terbalik (X naik maka Y turun). Data yang digunakan biasanya berskala interval atau rasio. Menurut Sugiyono (2007) pedoman untuk memberikan interpretasi koefisien korelasi sebagai berikut:

0,00 – 0,199 = sangat rendah

0,20 – 0,399 = rendah

0,40 – 0,599 = sedang

0,60 – 0,799 = kuat

0,80 – 1,000 = sangat kuat

Contoh kasus:
 

Kita mengambil contoh pada kasus korelasi sederhana di atas dengan menambahkan satu variabel kontrol. Seorang mahasiswa bernama Andi melakukan penelitian dengan menggunakan alat ukur skala. Andi ingin meneliti tentang hubungan antara kecerdasan dengan prestasi belajar jika terdapat faktor tingkat stress pada siswa yang diduga mempengaruhi akan dikendalikan. Dengan ini Andi membuat 2 variabel yaitu kecerdasan dan prestasi belajar dan 1 variabel kontrol yaitu tingkat stress. Tiap-tiap variabel dibuat beberapa butir pertanyaan dengan menggunakan skala Likert, yaitu angka 1=sangat tidak setuju, 2=tidak setuju, 3=setuju, dan 4=sangat setuju. Setelah membagikan skala kepada 12 responden didapatlah skor total item-item yaitu sebagai berikut:

Tabel Tabulasi Data (data fiktif)

Subjek Kecerdasan Prestasi Belajar Tingkat Stress

1 33 58 25

2 32 52 28

3 21 48 32

4 34 49 27

5 34 52 27

6 35 57 25

7 32 55 30

8 21 50 31

9 21 48 34

10 35 54 28

11 36 56 24

12 21 47 29 

3.2 Analisis Korelasi Product Moment

Digunakan untuk menentukan besarnya koefisien korelasi jika data yang digunakan berskala interval atau rasio. Rumus yang digunakan:

Contoh kasus:

Seorang mahasiswa melakukan survei untuk meneliti apakah ada korelasi antara pendapatan mingguan dan besarnya tabungan mingguan di P’Qerto.

Untuk menjawab permasalahan tersebut diambil sampel sebanyak 10 kepala keluarga.
Cara melakukan perhitungan manual uji korelasi di atas adalah sebagai berikut:

Asumsi uji korelasi

Sebelum diimplementasi, uji korelasi harus memenuhi serangkaian asumsi, yaitu:

1. Normalitas, artinya sebaran variabel-variabel yang hendak dikorelasikan harus berdistribusi normal.

2. Linieritas, artinya hubungan antara dua variabel harus linier, misalnya ditunjukkan lewat straight-line.

3. Ordinal, artinya variabel harus diukur dengan minimal skala ordinal.

4. Homoskedastisitas, artinya variabilitas skor di variabel Y harus tetap konstan di semua nilai variabel X.

Kriteria Penerimaan Hipotesis

H0 : tidak terdapat korelasi positif antara tabungan dengan pendapatan

Ha : terdapat korelasi positif antara tabungan dengan pendapatan

H0 diterima jika r hitung ≤ r tabel ( , n-2) atau t hitung ≤ ttabel ( , n-2)

Ha diterima jika r hitung > r tabel ( , n-2) atau t hitung > ttabel ( , n-2)

Sampel: 10 kepala keluarga

Data yang dikumpulkan:

Tabungan 2 4 6 6 8 8 9 8 9 10

pendapatan 10 20 50 55 60 65 75 70 81 85

Analisis data:

N Xi Yi Xi^2 Yi^2 XY

1 2 10 4 100 20

2 4 20 16 400 80

3 6 50 36 2500 300

4 6 55 36 3025 330

5 8 60 64 3600 480

6 8 65 64 4225 520

7 9 75 81 5625 675

8 8 70 64 4900 560

9 9 81 81 6561 729

10 10 85 100 7225 850

jumlah 70 571 546 38161 4544

Pengujian hipotesis:

Dengan kriteria r hitung: r hitung (0,981) > r tabel (0,707)

Dengan kriteria t hitung:

t hitung (14,233) > t tabel (1,86)

kesimpulan:
karena r hitung > dari r tabel maka Ha diterima, karena t hitung > t tabel maka Ha diterima
“terdapat korelasi positif antara pendapatan dengan tabungan mingguan di P’Qerto”

Pemikiran utama korelasi product momen adalah seperti ini:

1. Jika kenaikan kuantitas dari suatu variabel diikuti dengan kenaikan kuantitas dari variabel lain, maka dapat kita katakan kedua variabel ini memiliki korelasi yang positif. Jika kenaikan kuantitas dari suatu variabel sama besar atau mendekati besarnya kenaikan kuantitas dari suatu variabel lain dalam satuan SD, maka korelasi kedua variabel akan mendekati.

2. Jika kenaikan kuantitas dari suatu variabel diikuti dengan penurunan kuantitas dari variabel lain,maka dapat kita katakan kedua variabel ini memiliki korelasi yang negatif. Jika kenaikan kuantitas dari suatu variabel sama besar atau mendekati besarnya penurunan kuantitas dari variabel lain dalam satuan SD,maka korelasi kedua variabel akan mendekati -1.

3. Jika kenaikan kuantitas dari suatu variabel diikuti oleh kenaikan dan penurunan kuantitas secara random dari variabel lain atau jika kenaikan suatu variabel tidak diikuti oleh kenaikan atau penurunan kuantitas variabel lain (nilai dari variabel lain stabil), maka dapat dikatakan kedua variabel itu tidak berkorelasi atau memiliki korelasi yang mendekati nol.

           Dari pemikiran ini kemudian lahirlah Rumus Korelasi Product Momen Pearson seperti yang sering kita lihat di buku. Ada beberapa rumus yang dapat diacu. Semuanya akan memberikan hasil r yang sama, hanya saja dengan melihatnya kita akan dapat melihat pemaknaan yang berbeda-beda.

Ada beberapa hal yang dapat kita pelajari dari rumus ini :

Rumus pertama :

           Jika setiap subjek yang memiliki nilai X lebih rendah dari meannya, memiliki nilai Y yang juga lebih rendah dari meannya, nilai r akan menjadi positif. Begitu juga jika setiap subjek yang memiliki nilai X lebih tinggi dari meannya, memiliki nilai Y yang lebih tinggi dari meannya. Jika setiap subjek yang memiliki nilai X yang lebih tinggi dari meannya, memiliki nilai Y yang lebih rendah dari meannya maka nilai r akan menjadi negatif. Begitu juga jika tiap subjek yang memiliki nilai X lebih rendah dari meannya memiliki nilai Y yang lebih tinggi dari meannya. Jika tiap nilai X yang lebih tinggi dari meannya terkadang diikuti oleh nilai Y yang lebih tinggi terkadang lebih rendah dari meannya maka nilai r akan cenderung mendekati 0 (nol).

Rumus kedua:

          Dari rumus kedua ini dapat kita simpulkan bahwa nilai korelasi sebenarnya nilai kovarian dari dua variabel x dan y yang distandardkan dengan menggunakan standard deviasi x dan standard deviasi y sebagai denominatornya. Nilai kovarian sangat dipengaruhi oleh satuan skala yang digunakan oleh kedua variabel. Misalnya kita menghitung kovarian dari tinggi badan dengan panjang rambut , pengen tahu apakah tinggi badan berkorelasi dengan panjang rambut. Kita menghitung tinggi badan dan panjang rambut dalam satuan meter. Kemudian kita hitung kovariannya. Setelah itu kita menggunakan data yang sama, hanya mengubah satuannya menjadi centimeter, lalu menghitung kovariannya. Nah kovarian dari hasil perhitungan kedua akan terlihat lebih besar daripada yang pertama. Lebih besar? Ya karena dengan menggunakan satuan centimeter, 1.4 meter akan menjadi 140 centimeter. Jika kita hitung kovariannya, perhitungan pertama akan menghitung dalam skala satuan (1.4, 1.5, dst) sementara perhitungan kedua akan menghitung dalam skala ratusan. Oleh karena itu perlu distandardkan agar data yang sama akan menghasilkan angka yang sama meskipun diubah skalanya.

Rumus ketiga:

           Zx dan Zy itu berbicara mengenai nilai X dan Y dalam satuan SD. Jika nilai X ada di bawah mean dari X maka nilai Zx akan negatif, jika nilai X ada di atas meannya maka nilai Zx akan positif. Begitu juga dengan Y. Seperti pada rumus pertama, jika Zx dan Zy sepakat (keduanya positif atau negatif) maka nilai r akan positif. Jika Zx dan Zy berlawanan (jika yang satu positif yang lain negatif) maka nilai r akan negatif. Nah misalnya ada seratus subjek memiliki nilai X dan Y. Lalu kita hitung satu-satu nilai Z dari X dan Y untuk tiap subjek. Tentu saja ada beberapa yang sangat sepakat yang lain agak sepakat yang beberapa berlawanan. Kemudian nilai-nilai Z ini dijumlahkan sehingga jika yang sepakat lebih banyak akan menghasilkan angka positif. Kalo yang berlawanan lebih banyak akan menghasilkan angka negatif. Kemudian hasil penjumlahan ini dicari rata-ratanya. Jadi bisa dibilang nilai r itu akan menggambarkan rata-rata keadaan X dan Y dari semua subjek dalam kelompok.

A.    REGRESI 

1. PENGERTIAN

 

Analisis regresi dalam statistika adalah salah satu metode untuk menentukan hubungan sebab-akibat antara satu variabel dengan variabel(-variabel) yang lain. Variabel “penyebab” disebut dengan bermacam-macam istilah: variabel penjelas, variabel eksplanatorik, variabel independen, atau secara bebas, variabel X (karena seringkali digambarkan dalam grafik sebagai absis, atau sumbu X). Variabel terkena akibat dikenal sebagai variabel yang dipengaruhi, variabel dependen, variabel terikat, atau variabel Y. Kedua variabel ini dapat merupakan variabel acak (random), namun variabel yang dipengaruhi harus selalu variabel acak. Analisis regresi adalah salah satu analisis yang paling populer dan luas pemakaiannya. Hampir semua bidang ilmu yang memerlukan analisis sebab-akibat boleh dipastikan mengenal analisis ini.

2. KEGUNAAN

Tujuan menggunakan analisis regresi ialah:

-Membuat estimasi rata-rata dan nilai variabel tergantung dengan didasarkan pada nilai variabel bebas.

-Menguji hipotesis karakteristik dependensi

-Untuk meramalkan nilai rata-rata variabel bebas dengan didasarkan pada nilai variabel bebas diluar jangkaun sample.

 

3. ANALISIS REGRESI

3.1 Analisis Regresi Berganda

            Regresi berganda seringkali digunakan untuk mengatasi permasalahan analisis regresi yang melibatkan hubungan dari dua atau lebih variabel bebas. Pada awalnya regresi berganda dikembangkan oleh ahli ekonometri untuk membantu meramalkan akibat dari aktivitas-aktivitas ekonomi pada berbagai segmen ekonomi. Misalnya laporan tentang peramalan masa depan perekonomian di jurnal-jurnal ekonomi (Business Week, Wal Street Journal, dll), yang didasarkan pada model-model ekonometrik dengan analisis berganda sebagai alatnya. Persamaan regresi linear berganda sebagai berikut:

Y’ = a+b1X1+b2X2+….+ bnXn

Keterangan:
Y’ : variabel dependen (nilai yag diprediksikan)

X1 dan X2 : variabel independen

a : konstanta

b : koefisien regresi(nilai peningkatan/penurunan)

contoh kasus:

Seorang peneliti ingin mengetahui pengaruh dari tinggi badan terhadap berat badan. Untuk kebutuhan penelitian tersebut diambil sampel secara acak sebanyak 10 orang untuk diteliti. Hasil pengumpulan data diketahui data sebagai berikut :

Berdasarkan data tersebut di atas :

Hitunglah nilai a dan b untuk persamaan regersi linier sederhana. Jika hipotesis penelitian menyatakan bahwa “tinggi badan seseorang berpengaruh terhadap berat badan seseorang”, ujilah hipotesis tersebut dengan menggunakan Uji T dan Uji F (tingkat keyakinan sebesar 95%). Hitunglah nilai r dan koefisien determinasi. Bagaimana kesimpulannya !

Jawab :

Hipotesis penelitian : Tinggi Badan berpengaruh terhadap Berat Badan Seseorang (karena hanya dikatakan berpengaruh maka menggunakan uji dua arah).

Jika Y : Berat Badan Seseorang dan X : Tinggi Badan Seseorang, maka untuk mendapatkan nilai a dan b untuk persamaan regersi linier sederhana :

Berdasarkan hasil pengolahan data tersebut di atas maka dapat dibuat persamaan regresi linier sederhana : Y = – 73,72041 + 0,819657 X

Untuk menguji hipotesis secara parsial digunakan Uji T, yaitu :

Hipotesis Statistik adalah Ho : b = 0 dan Ha : b ≠ 0 (disebut uji dua arah)

Nilai T hitung adalah : b/Sb = 0,819657/0,05525673 = 14,833613932638 = 14,834

Nilai T tabel dengan df : 10 – 2 = 8 dan ½ α = 2,5% (uji dua arah) sebesar ± 2,306

Karena nilai T hitung lebih besar dari pada T tabel atau 14,834 > 2,306 maka Ho ditolak, Ha diterima dan hipotesis penelitian yang menyatakan bahwa Tinggi Badan berpengaruh terhadap Berat Badan Seseorang adalah dapat diterima (dapat dikatakan signifikan secara statistik).
Sedangkan untuk menguji secara serempak digunakan Uji F, yaitu diperoleh F hitung = 31.874,98 dan Untuk nilai F tabel dengan df : k – 1 ; n – k = 1 ; 8 dan α : 5% sebesar 5,32. Karena nilai F hitung lebih besar dari F tabel atau 31.874,98 > 5,32 maka Ho ditolak, Ha diterima dan hipotesis penelitian yang menyatakan bahwa Tinggi Badan berpengaruh terhadap Berat Badan Seseorang adalah dapat diterima.

3.3 Analisis Regresi Sederhana

            Regresi Linier Sederhana Regresi linier sederhana bertujuan mempelajari hubungan linier antara dua variabel. Dua variabel ini dibedakan menjadi variabel bebas (X) dan variabel tak bebas (Y). Variabel bebas adalah variabel yang bisa dikontrol sedangkan variabel tak bebas adalah variabel yang mencerminkan respon dari variabel bebas.

            Statistik regresi dapat didapatkan dengan berbagai cara, diantaranya ialah dengan menggunakan metode tangan bebas dan metode kuadrat terkecil. Dengan menggunakan metode kuadrat terkecil maka nilai a dan b dapat langsung dicari menggunakan rumus di bawah ini:

Contoh:
Diketahui peubah nilai skor tes masuk (X) dengan nilai ekonomi (Y) sebagai berikut:

Mahasiswa Skor tes (X) Nilai ekonomi (Y)

1 65 65

2 50 74

3 55 76

4 65 90

5 55 85

6 70 87

7 65 94

8 70 98

9 55 81

10 70 91

11 50 76

12 55 74

Berdasarkan data diatas tentukan hubungan matematis antara skor tes masuk dengan nilai ekonomi.

Jawaban:

Sehingga persamaan regresinya ialah:

Y= 30,056 + 0,897 X

SUMBER : 

 http://fariidaelf.wordpress.com/materi-kuliah/korelasi-regresi/

ANALISIS VARIANSI

1. Pengertian Anova
 Analisis varians (analysis of variance, ANOVA) adalah suatu metode analisis statistika yang termasuk ke dalam cabang statistika inferensi. Dalam literatur Indonesia metode ini dikenal dengan berbagai nama lain, seperti analisis ragam, sidik ragam, dan analisis variansi. Ia merupakan pengembangan dari masalah Behrens-Fisher, sehingga uji-F juga dipakai dalam pengambilan keputusan. Analisis varians pertama kali diperkenalkan oleh Sir Ronald Fisher, bapak statistika modern. Dalam praktik, analisis varians dapat merupakan uji hipotesis (lebih sering dipakai) maupun pendugaan (estimation, khususnya di bidang genetika terapan).
Berikut Hipotesis dalam anova :
H0: μ1 = μ2 = μ3 = ... = μn, Tidak ada perbedaan yang nyata antara rata-rata hitung dari n kelompok
H1: μ1 ≠ μ2 ≠ μ3 ≠ ... ≠ μn, Ada perbedaan yang nyata antara rata-rata hitung dari n kelompok

Uji hipotesis dengan ANOVA digunakan, setidaknya karena beberapa alasan berikut:

1. Memudahkan analisa atas beberapa kelompok sampel yang berbeda dengan resiko kesalahan terkecil.
2. Mengetahui signifikansi perbedaan rata-rata (μ) antara kelompok sampel yang satu dengan yang lain. Bisa jadi, meskipun secara numeris bedanya besar, namun berdasarkan analisa ANOVA, perbedaan tersebut TIDAK SIGNIFIKAN sehingga perbedaan μ bisa diabaikan. Sebaliknya, bisa jadi secara numeris bedanya kecil, namun berdasarkan analisa ANOVA, perbedaan tersebut SIGNIFIKAN, sehingga minimal ada satu μ yang berbeda dan perbedaan μ antar kelompok sampel tidak boleh diabaikan.
3. Analisis varians relatif mudah dimodifikasi dan dapat dikembangkan untuk berbagai bentuk percobaan yang lebih rumit. Selain itu, analisis ini juga masih memiliki keterkaitan dengan analisis regresi. Akibatnya, penggunaannya sangat luas di berbagai bidang, mulai dari eksperimen laboratorium hingga eksperimen periklanan, psikologi, dan kemasyarakatan.

2. Jenis-jenis Anova

Sesuai dengan banyaknya faktor yang terlibat, maka anava dibedakan secara garis besar menjadi dua yaitu :

1)      Anava tunggal atau anova satu jalan

2)      Anava ganda atau anova lebih dari satu jalan.

-Analisis Variansi Satu Jalur-

 Yang dimaksud dengan analisis varians satu jalan adalah analisis varians yang digunakan untuk mengolah data yang hanya mengenal satu variable pembanding.

Dinamakan analisis varians satu arah, karena analisisnya menggunakan varians dan data hasil pengamatan merupakan pengaruh satu faktor.Dari tiap populasi secara independen kita ambil sebuah sampel acak, berukuran n₁ dari populasi kesatu, n₂ dari populasi kedua dan seterusnya berukuran n_k dari populasi ke k. Data sampel akan dinyatakan dengan Y_ij yang berarti data ke-j dalam sampel yang diambil dari populasi ke-i. ( Sudjana.1996.Metoda Statistika.Bandung:Tarsito Bandung).

ANAVA satu jalur yaitu analisis yang melibatkan hanya satu peubah bebas. Secara rinci, ANAVA satu jalur digunakan dalam suatu penelitian yang memiliki ciri-ciri berikut:1. Melibatkan hanya satu peubah bebas dengan dua kategori atau lebih yang dipilih dan ditentukan oleh peneliti secara tidak acak. Kategori yang dipilih disebut tidak acak karena peneliti tidak bermaksud menggeneralisasikan hasilnya ke kategori lain di luar yang diteliti pada peubah itu. Sebagai contoh, peubah jenis kelamin hanya terdiri atas dua ketgori (pria-wanita), atau peneliti hendak membandingkan keberhasilan antara Metode A, B, dan C dalam meningkatkan semangat belajar tanpa bermaksud menggeneralisasikan ke metode lain di luar ketiga metode tersebut.

1.             Perbedaan antara kategori atau tingkatan pada peubah bebas dapat bersifat kualitatif atau kuantitatif.

2.             Setiap subjek merupakan anggota dari hanya satu kelompok pada peubah bebas, dan dipilih secara acak dari populasi tertentu. (Furqon. 2009. Statistika Terapan untuk Penelitian. Cetakan ketujuh. ALFABETA: Bandung)

Tujuan dari uji anova satu jalur adalah untuk membandingkan lebih dari dua rata-rata. Sedangkan gunanya untuk menguji kemampuan generalisasi. Maksudnya dari signifikansi hasil penelitian. Jika terbukti berbeda berarti kedua sampel tersebut dapat digeneralisasikan (data sampel dianggap dapat mewakili populasi). Anova satu jalur dapat melihat perbandingan lebih dari dua kelompok data. (Riduwan.2008.Dasar-dasar Statistika.Bandung:Alfabeta)

Anova pengembangan atau penjabaran lebih lanjut dari uji-t .Uji-t atau uji-z hanya dapat melihat perbandingan dua kelompok data saja. Sedangkan anova satu jalur lebih dari dua kelompok data. Contoh: Perbedaan prestasi belajar statistika antara mahasiswa tugas belajar (X1), izin belajar (X2) dan umum (X3).

Anova lebih dikenal dengan uji-F (Fisher Test), sedangkan arti variasi atau varian itu asalnya dari pengertian konsep “Mean Square” atau kuadrat rerata (KR).

Rumusnya :

KR=JK/db

Dimana: JK = jumlah kuadrat (some of square)

                 db  = derajat bebas (degree of freedom)

-Analisis Variansi Dua Jalur-
Analisis varians dua jalan merupaka teknik analisis data penelitian dengan desain faktorial dua faktor. Dalam penelitian ini terdapat dua variable yang digunakan untuk dasar peninjauan sekor utntuk variable terikat. Anava dua jalan mempunyai judul kolom dan judul baris dengan menggunakan klasifikasi dua variable yang digunakan sebagai dasar tinjauan sekor untuk variable terikat. Anava dua jalan yang juga disebut dengan anava modal AB mempunyai dua variabel. Model diagram analisis dua jalan dapat berupa dua alternative.
Two way ANOVA digunakan untuk menguji hipotesis komparatif rata-rata k sampel bila peneliti melakukan kategorisasi terhadap sampel kedalam beberapa blok, sehingga bila variabilitas atau sumber keragaman pada uji One Way ANOVA berasal dari perlakuan dan galat, maka pada two way ANOVA sumber keragaman tidak hanya berasal dari perlakuan dan galat, tapi juga berasal dari blok.

Berikut adalah langkah-langkah dalam perhitungan ANOVA dua jalur (two way ANOVA):

1. Identifikasi nilai: t (jumlah perlakuan), r (jumlah blog),
2. hitung jumlah pengamatan total (n), yaitu: n = r x t,
3. Hitung jumlah kuadrat total dengan rumus:
   
4. Hitung jumlah kuadrat perlakuan dengan rumus:
   
5. Hitung jumlah kuadrat antar blok dengan rumus:
   
6. Cari harga F-Hitung dengan menggunakan rumus yang tertera pada tabel.
   

7. Cari harga F tabel dengan mempertimbangkan (1) tingkat signifikansi (α), (2) df1 yaitu df dari MS terbesar, dan (3) df2 yaitu df dari MS terkecil.
8. Bandingkan harga F Hitung dengan F tabel.
   (1) Bila F Hitung < F tabel, maka Ho diterima, yang berarti rata-rata kedua perlakuan tidak berbeda secara signifikan,
   (2) Bila F Hitung > F tabel, maka Ho ditolak dan H1 diterima, yang berarti rata-rata kedua perlakuan berbeda secara signifikan.

Untuk lebih jelasnya, lihat contoh kasus berikut:
Seorang peneliti ingin mengetahui apakah ada pengaruh yang signifikan dari beberapa jenis pupuk (pupuk A, B, C, D, E dan F) terhadap pertumbuhan tanaman jagung di sebuah wilayah. Peneliti tersebut kemudian membagi petak percobaan kedalam 3 blok berdasarkan tingkat kesuburannya, yaitu: I= tingkat kesuburan rendah, 2= sedang, dan 3 = tinggi. Penelitian disusun berdasarkan desaian Rancangan Acak Kelompok, dan yang menjadi parameter adalah bobot tongkol jagung (g).

Setelah dilakukan pengukuran terhadap berat tongkol jagung, maka diperoleh hasil sebagai berikut:

Untuk mengetahui apakah ada perbedaan signifikan antar perlakuan, maka dilakukan uji ANOVA 2 arah (two way ANOVA). Proses pengerjaannya dapat dilakukan secara cepat dan mudah dengan menggunakan aplikasi program Microsoft Excel.


 http://statistikceria.blogspot.com/2013/12/uji-hipotesis-dengan-analisis-ragam-analysis-of-variance-anova.html
http://pratiwikalit.blogspot.com/2011/03/analisis-varians.html
 www.slideshare.net/yusrinans/anova-satu-jalur-revisi‎
 http://freelearningji.wordpress.com/2013/04/11/anova-dua-jalur-two-way-anova/

PENGUJIAN HIPOTESIS

1.     Pengertian Hipotesis

Hipotesa berasal dari penggalan kata ”hypo” yang artinya ”di bawah” dan thesa” yang artinya ”kebenaran”, jadi hipotesa yang kemudian cara menulisnya disesuaikan dengan ejaan Bahasa Indonesia menjadi hipotesa dan berkembangan menjadi Hipotesa.

Hipotesis merupakan dugaan/ pernyataan sementara yang diungkapkan secara deklaratif/ yang menjadi jawaban dari sebuah permasalahan.  Pernyataan tersebut diformulasikan dalam bentuk variabel agar bisa di uji secara empiris. Hipotesis merupakan identik dari perkiraan atau prediksi. Dari sebuah hipotesis maka akan menimbulkan suatu prediksi, karena prediksi adalah hasil yang diharapkan diperoleh dari hipotesis. Hipotesis dapat diketahui jika telah melakukan suatu percobaan sehingga mengetahui hasilnya. Salah satu langkah dalam penelitian menggunakan metodo ilmiah adalah hipotesis. Seorang ilmuan/ peneliti haruslah mempunyai kemampuan untuk memprediksi suatu permasalahan. Mungkin anda sering mendengar mengenai perkiraan cuaca, perkiraan iklim yang sering disiarkan di televise ataupun di radio, di internet dan lain-lain. Itu dilakukan oleh para ahli meteorology, mereka dapat memprediksi/ memperkirakan cuaca yang akan terjadi di suatu daerah pada suatu hari dengan cara melakukan observasi menggunakan pengetahuan yang mereka miliki. Maka kemampuan memprediksi merupakan ketrampilan yang harus dimiliki oleh seorang ilmuan.

2.    Langkah Pengujian Hipotesis

Suatu hipotesis harus dapat diuji berdasarkan data empiris, yakni berdasarkan apa yang dapat diamati dan dapat diukur. Untuk itu peneliti harus mencari situasi empiris yang memberi data yang diperlukan. Setelah kita mengumpulkan data, selanjutnya kita harus menyimpulkan hipotesis , apakah harus menerima atau menolak hipotesis. Ada bahayanya seorang peneliti cenderung untuk menerima atau membenarkan hipotesisnya, karena ia dipengaruhi bias atau perasangka. Dengan menggunakan data kuantitatif yang diolah menurut ketentuan statistik dapat ditiadakan bias itu sedapat mungkin, jadi seorang peneliti harus jujur, jangan memanipulasi data, dan harus menjunjung tinggi penelitian sebagai usaha untuk mencari kebenaran. 

Adapun langkah-langkahnya adalah sebagai berikut :

1. Nyatakan hipotetsis nolnya H₀ bahwa q = q_o ,
2. Pilih hipotetsis alternative atau lawan hipotesis awal H₁ yang sesuai q ¹ q_o, q > q₀ ,q < q_o
3. Tentukan taraf signifikan a.
4. Pilih statistic uji yang digunakan apakah z, t, c² , F atau lainnya.
5. Tentukan wilayah ktitisnya atau daerah penolakan Ho
6. Perhitungan nilai statistic uji berdasarkan sample.
7. Kesimpulan, yaitu Keputusan antara tolak H₀ atau terima Ho.

3.    Jenis-jenis Hipotesis

a.    Hipotesis deskriptif (pada satu sampel/variabel mandiri/tidak dibandingkan dan dihubungkan)

b.    Hipotesis komparatif

c.    Hipotesis hubungan

1.    Hipotesis Deskriptif

Hipotesis yang tidak membandingkan dan menghubungkan dengan variable lain atau hipotesis yang dirumuskan untuk menggambarkan suatu fenomena, atau untuk menjawab permasalahan taksiran.

Dalamperumusan hipotesis statistik, antara hipotesis nol (Ho) dan hipotesis alternatif (Ha) selalu berpasangan, bila salah satu ditolak, maka yang lain pasti diterima sehingga dapat dibuat keputusan yg tegas, yaitu kalau Ho ditolak, pasti Ha diterima.

-Contoh : Suatu bimbingan tes menyatakan bahwa murid yg dibimbing di lembaga itu paling sedikit 90% dapat diterima di Perguruan Tinggi Negeri. Rumusan hipotesis statistiknya :

Ho : µ ≥ 0,90

Ha : µ < 0,90

  

 2.    Hipotesis Komparatif

Hipotesis yang dirumuskan untuk memeberikan jawaban pada permasalahn yang bersifat membedakan atau membandingkan antara satu dengan data lainnya.

-Contoh :

Rumusan masalah komparatif : Apakah ada perbedaan produktifitas kerja antara pegawai golongan I, II, dan III?

Rumusan hipotesis : Tidak terdapat perbedaan (ada persamaan) produktifitas kerja antara pegawai golongan I, II, dan III.

Rumusan hipotesis statistiknya :

Ho : µ₁ = µ₂ = µ₃

Ha : µ₁ ≠ µ₂ = µ₃ (salah 1 berbeda merupakan Ha)

     3.    Hipotesis Asosiatif

Hipotesis yang dirumuskan untuk memberikan jawaban pada permasalahan yang bersifat hubungan / pengaruh. Sedangkan menurut sifat hubungannya hipotesis ini dibagi tiga jenis yaitu.

a.    Hipotesis hubungan simetris

Hipotesis yang menyatakan hubungan bersifat kebersamaan antara dua variable atau lebih tetapi tidak menunjukkan sebab akibat.

Contoh.

1.    Ada hubungan antara berpakaian mahal dengan penampilan

2.    Terdapat hubungan yang positif antara banyaknya peserta didik rajin belajar dengan tingkat intelegensi (IQ)

b.    Hipotesis hubungan sebab akibat (kausal)

Hipotesis yang menyatakan hubungan bersifat sebab akibat antara dua variable atau lebih

Contoh.

1.    Tingkat pengangguran berhubungan dengan tingkat kriminalitas

2.    Tingkat keberhasilan peserta didik bergantung pada cara belajar peserta didik itu sendiri

c.    Hipotesis hubungan interaktif

Hipotesis hubungan antara dua variable atau lebih bersifat saling mempengaruhi.

Contoh.

1.    Terdapat hubungan yang saling mempengaruhi antara status peserta didik sebagai anak pejabat dengan cara belajar peserta didik di sekolah.

2.    Terdapat pengaruh timbal balik antara kreativitas peserta didik dengan hasil belajar

Sumber :

http://iwan24.blogspot.com/

http://temukanpengertian.blogspot.com/2013/06/pengertian-hipotesis.html

http://cerdaskan.com/langkah-langkah-pengujian-hipotesis.html

http://khadijahtabrani.blogspot.com/2012/12/jenis-hipotesis-penelitian_15.html

Sugiyono.(2012).Statistika untuk Penelitian.Bandung:Alfabeta